Progetto completo scale in cemento armato NTC 18 - a ginocchio
Di seguito il progetto completo di verifiche agli stati limite ultimi, di esercizio e deformazioni in cemento armato di una scala a ginocchio secondo le nuove normative tecniche sulle costruzioni NTC del 2018.
Premessa
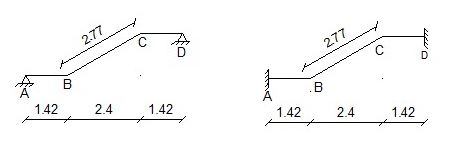
La scala interna è costituita da due rampe identiche di otto gradini ciascuna, intervallate da un pianerottolo.
La scala viene realizzata nella tipologia a doppio ginocchio per entrambe le rampe, ed esse hanno una larghezza di 120 cm sulla quale appoggiano gli scalini.
Il pianerottolo è anch’esso costituito da una soletta portante di spessore 20 cm.
Ciascun gradino ha alzata h pari a 17 cm e pedata p pari a 30 cm, in modo che risulti rispettato il criterio di buona progettazione:
62 cm ≤ 2∙h+p ≤ 64 cm
L’inclinazione della soletta risulta di 30°.
RAMPA E PIANEROTTOLI
Analisi dei carichi
I carichi agenti sul pianerottolo e sulla rampa derivano dall’analisi dei carichi svolta al capitolo 2:
Pianerottolo:
- Peso proprio del pianerottolo: 5 kN/mq
- Carichi permanenti sul pianerottolo: 1.68 kN/mq
- Sovraccarico d’uso: 4 kN/mq
Rampa:
- Peso proprio della rampa: 5 kN/mq
- Carichi permanenti sulla rampa: 2.73 kN/mq
- Sovraccarico d’uso: 4 kN/mq
Schema statico e combinazione di carico
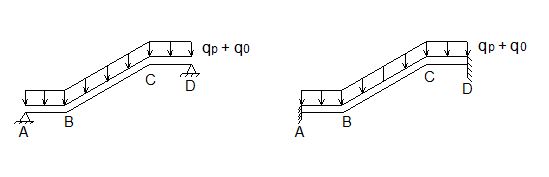
Calcolo delle sollecitazioni
Combinazioni agli SLU:

Verifica agli SLU per presso-flessione
Sul pianerottolo non sono presenti sforzi normali, la soletta presenta invece, oltre le sollecitazioni di taglio e di momento, anche sforzi normali, sia di compressione che di trazione.
Poiché sia i pianerottoli che la soletta verranno armati allo stesso modo, verrà condotta un’unica verifica, agli SLU per presso flessione.
La verifica agli SLU per presso-flessione consiste nel tracciare il dominio di resistenza (NRdu;MRdu) delle sezioni dei pilastri e verificare che le coppie sollecitanti (NEd;MEd), in ogni sezione significativa degli stessi, siano contenute nel suddetto dominio. Il dominio di resistenza rappresenta infatti le infinite coppie che portano la sezione a rottura, e di conseguenza delimita la zona di utilizzo della sezione.
Vengono assunte le seguenti leggi costitutive:
- legge elastica – perfettamente plastica per l’acciaio
- legge dello stress – block per il calcestruzzo
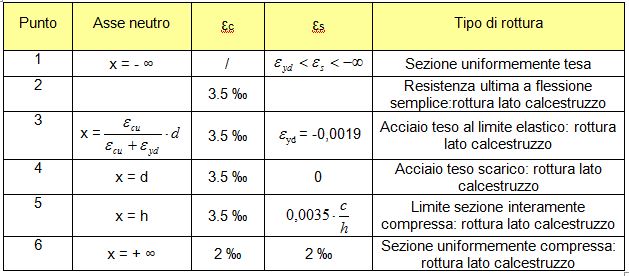
Per la determinazione del dominio di resistenza si individuano alcuni punti appartenenti ad esso, relativi a diverse posizioni dell’asse neutro:
Verifica agli SLU per presso-flessione degli elementi del pianerottolo
Per ciascuna sezione le coppie di valori che devono esser verificate sono:
(NEd, MEd)A = (0; -49,8)
(NEd, MEd)B = (13.8; 57.3)
(NEd, MEd)C = (-13.8; 57.3)
(NEd, MEd)D = (0; -49.8)
Si adottano 8xφ14 sia per l’armatura superiore che per quella inferiore, di area resistente As = A’s = 1231,12 mmq
La geometria della sezione su cui si andranno ad effettuare le verifiche è dunque la seguente:
b = 1200 mm base della sezione
h = 200 mm altezza totale della sezione
d = 155 mm altezza utile
d’= 45 mm
A’s = 1231,12mmq quantitativo di armatura superiore
As = 1231,12mmq quantitativo di armatura inferiore
Poiché la sezione è simmetrica rispetto all’asse momento in quanto è simmetrica sia la casseratura sia l’armatura, il dominio di resistenza risulterà simmetrico rispetto all’asse degli sforzi normali:
PUNTO 1: sezione uniformemente tesa, acciaio snervato

PUNTO 2 resistenza ultima a flessione semplice
Per il calcolo di tale punto del dominio si ipotizza la rottura lato calcestruzzo, l’armatura inferiore snervata e quella superiore non snervata.
Si calcola quindi la posizione dell’asse neutro imponendo l’equilibrio alla traslazione (condizione Nrdu=0):
Ipotesi:
Continua a leggere il file su word